Lịch sử con số Pi bí ẩn diệu kỳ

Vietsciences-Võ Thị Diệu Hằng        13/05/2006    
 

Định nghĩa:

Pi = 3,142592653589793238462643383279....

  • Số Pi là tên của chữ thứ  16 của mẫu tự Hy lạp. Nó được định nghĩa như một hằng số , là tỷ số giữa chu vi vòng tròn với đường kính của nó.

  • Tên pi  do chữ peripheria (perijeria) có nghĩa là  chu vi của vòng tròn.

  • Nhưng nó  không  có tên chính xác, thường người ta  gọi là Pi, c, hay p

  •  Chữ  Pi được dùng  vào khoảng  giữa thế kỷ thứ 18, sau khi Euler xuất bản cuốn chuyên luận phân tích năm 1748. Ý định dùng ký hiệu  Pi là để tưởng nhớ đến những nhà Toán học Hy Lạp là những người tìm ra đầu tiên con số gần đúng của  pi

  • Cuối thế kỷ thứ 20 số Pi đã tính với độ chính xác tới con số thứ 200 tỉ (200 000 000 000)

  • 11 tháng  9 năm  2000: con số lẻ thứ một triệu tỉ (1.000.000.000.000.000) là số không
     

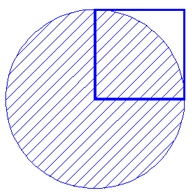
Định nghĩa đơn giản nhất mà người ta cho con số nổi tiếng này là: nó là tỷ số giữa diện tích dĩa tròn và bình phương bán kính. Thí dụ, diện tích dĩa tròn của hình bên đây bằng Pi lần diện tích của hình vuông.

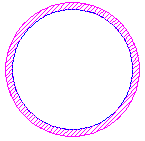
Người ta lại tìm thấy cũng con số ấy trong phép tính chu vi của vòng tròn, bằng 2 Pi lần bán kính của nó. Cũng như Archimède đã nhận xét, con số đó dùng cho hai phép tính này. Và cũng  không gì đáng ngạc nhiên nếu ta lại gặp cũng con số ấy đây đó:

*diện tích của vành nằm giữa hai vòng tròn có bán kính gần  bằng nhau, có thể được tính bằng hai cách:

- Lấy diện tích dĩa tròn lớn trừ diện tích dĩa tròn nhỏ

- Vì bán kính của hai vòng tròn gần bằng nhau nên diện tích vành là tích số giữa chu vi của một trong hai vòng tròn với chiều dày của vành.

 

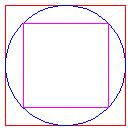
Các phương pháp  tính số Pi

Phép tính gần đúng:

Phương pháp cổ xưa nhất:

Vẽ một vòng tròn bán kính là 1 đơn vị và hai đa giác đều nội tiếp và ngoại tiếp của vòng tròn. 

Nếu đa giác đều đó là hình vuông thì trĩ số chu vi hình tròn sẽ ở giữa chu vi hình vuông nội tiếp và ngoại tiếp, nghĩa là trị số của Pi sẽ : 

2 < Pi < 4

 2,828 < Pi < 4

 

Tăng số cạnh lên 6 ta có kết quả khá hơn: 3 (Bởi vì cạnh hình lục giác bằng bán kính vòng tròn) và 2= 3,461...:  

 3< Pi <  2

 3 < Pi < 3,461

 

Khi tính chu vi các đa giác có hàng ngàn cạnh, và chia kết quả cho đường kính của vòng tròn, ta tìm được giá trị xấp xỉ chính xác nhất của Pi là 355/113

3 5 5
1 1 3

Con số dễ nhớ: là những số lẻ đầu tiên, 2 con số 3, hai con số 5, hai con số 1 và tổng số hai số của tử số và mẫu số chéo nhau sẽ bằng 6

 

 

 

Người Babylone tính được con số Pi bằng cách so sánh chu vi của một vòng tròn với đa giác nội tiếp trong vòng tròn đó, bằng 3 lần đường kính vòng tròn. Họ tính phỏng chừng: Pi = 3 + 1/8 (tức là 3,125)

Archimède đã dùng một đa giác có 96 cạnh, đã tính được số phỏng chừng nhỏ hơn (inférieur) là  3 + (10/71) = 3,1408...  và số phỏng chừng lớn hơn là 3 + (1/7) = 3,1429... 

nghĩa là

3,1408...<  Pi < 3,1429...

Để định giá trị của Pi, người ta  có thể thử vẽ một dĩa tròn và một hình vuông có cùng diện tích bằng cách dùng thước  và compas. Và cũng dùng  thước và compas, ta vẽ đoạn thẳng có chiều dài là Pi, rồi suy ra trị số chính xác của số này.

 Nhưng cách vẽ này không thể có được: Năm 1837, Pierre Wantzel chứng minh rằng người ta chỉ có thể vẽ các đoạn thẳng bằng thước và compas khi chiều dài là một số đại số, nghĩa là một đáp số từ một phương trình đại số mà hệ số (coefficient) là những số nguyên,

và năm 1882, Ferdinand von Lindermann chứng  minh rằng số Pi không  phải là số đại số.

Số Pi được tìm thấy trong nhiều ngành toán khác:

 * Thí dụ khi ta  đo góc, phải chọn một đơn vị bằng cách tự ý định nguyên một vòng 360, thì với đơn vị "độ" sẽ có số đo là 1/360 vòng. Nếu ta dùng trị số một vòng bằng 2Pi, thì đơn vị đo lường sẽ được gọi là radian và có trị số bằng 1/(2Pi). Đo góc  bằng radian có nhiều lợi thế hơn: thí dụ chiều dài một phần của vòng tròn được giới hạn bởi góc a sẽ bằng ra khi ta đo góc bằng radian, nhưng  nếu đo bằng độ, sẽ bằng (2Pira)/360

 

 

 

* Tương tự, tỉ số (sinx)/x tiến tới 1 khi x tiến tới 0 nếu ta tính các góc bằng radian, nhưng  sẽ tiến tới 180/Pi nếu ta tính góc  bằng độ.

* Cách dùng radian để đo góc suy ra được nhiều đặc tính của số Pi, thí dụ theo định lý Euler thì exponentiel của số phức 2iPi thì bằng 1. Và cũng từ kết quả việc dùng radian để tính góc, người ta tìm thấy số Pi ở những  nơi bất ngờ: thí dụ tổng số vô hạn (dãy số Leibniz série de Leibniz)

1 - (1/3) + (1/5) - (1/7) - ...   có trị số bằng  Pi/4.

* Tích phân:

nghĩa là diện tích dưới đường cong của phương trình f(x) = 1/(1+ x2)  giữa 0 và 1 cũng bằng  Pi/4. Hai kết quả này được giải nghĩa không  mấy khó khăn vì tiếp tuyến của góc Pi/4 bằng 1

Số Pi cũng xuất hiện trong trị số của tổng số

 1 + (1/22  ) + (1/32  ) + (1/42  ) + ...   bằng  Pi/6

 

Những số lẻ  của số Pi

Con số Pi tóm tắt một lịch sử về toán học cổ xưa hơn 4000 năm bao trùm Hình học phân tích hay Ðại số.

Các nhà Toán học đã hâm mộ nó từ thời Văn minh Cổ-đại và đặc biệt những người Hy Lạp trong vấn đề hình học.

Tri giá xưa nhất về con số Pi mà con người đã dùng và đã được chứng nhận từ một tấm bảng

Về sau, những công trình nghiên cứu liên tục:

* Archimède tính được số Pi = 3,142 với độ chính xác là 1/1000. Công thức là: 3 + 10/71 < Pi < 3 + 1/7

Người ta dùng phương pháp Archimède trong 2000 năm.

* Trong Thánh Kinh, khoảng 550 trước TC, đã giấu con số này trong một câu văn ở một tấm bảng của người Babylone cổ xưa (thuộc xứ Iraque) có chữ hình góc (écriture cunéiforme), được khám phá năm 1936 và tuổi của tấm bảng là 2000 năm trước Thiên Chúa. Sau bao nhiêu bộ óc tò mò tìm kiếm mới ra con số Pi = 3,141509

* Khoảng năm 1450, Al'Kashi tính con số Pi với 14 con số lẻ nhờ phương pháp đa giác của Archimède

Ðó là lần đầu tiên trong lịch sử nhân loại đã tìm được con số Pi với trên 10 số lẻ.

* Năm 1609 Ludolph von Ceulen nhờ phương pháp của Archimède, đã tính được con số Pi với 34 số lẻ mà người ta đã khắc số này trên mộ bia của ông.
Không thể tính trị số chính xác của số Pi.

Cuối thế kỷ thứ 18, Johann Heinrich Lambert (1728-1777) và Adrien-Marie Legendre (1752-1833) chứng minh rằng không có một phân số nào để tính số Pi .

Thế kỷ thứ 19, Lindemann  chứng minh rằng số Pi không thể là một nghiệm số của một phương trình đại số với hệ số là số nguyên (thí dụ y = ax2 +bx + c mà a, b, c là số nguyên)

* Kế tiếp Ludolph von Ceulen nhờ những công trình nghiên cứu miệt mài của các nhà Toán học:

Newton (1643-1727)

Leibniz (1646-1716)

Grégory (1638-1675)


Các nhà khoa học Euler (1707-1783), Gauss, Leibniz, Machin, Newton, Viète   tìm kiếm những công thức để tính trị số xấp xỉ của Pi cho chính xác. Và công thức giản dị nhất được Leibniz tìm ra năm 1674 là:

Pi/4 = 1 - 1/3 + 1/5 - 1/7 + ...


Carl Louis Ferdinand von Lindemann (1852-1939)

Srinivasa Aiyangar Ramanujan (1887-1920)

Williams Shanks (1812-1882) đã tính năm 1874 với 707 số lẻ

 Phải đợi đến thế kỷ thứ 18 và đầu thế kỷ thứ 20 thì số Pi đã được tính với độ chính xác là 1000 số lẻ.
Năm 1995, Hyroyuki Gotu đã chiếm kỷ lục thế giới : tìm ra 42 195 con số lẻ.

 

Niềm đam mê con số bí ẩn:

Một trăm số lẻ đầu tiên của Pi:

3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 0679 ...

Daniel Morin ghi 2000 số lẻ của Pi trong trang

  http://platon.lacitec.on.ca/~dmorin/divers/pi.html

100 000 số lẻ được ghi ở trang của Yves Martin:

 http://www.nombrepi.com/pi100000.html

Năm 1995 Yves Martin đã dùng máy vi tính xách tay hiệu EPSON , vận tốc 10 MHz, cho chạy chương trình PIF.EXE viết bằng ngôn ngữ Pascal, chạy trong 1 giờ 28 phút 33 giây  để cho ra 130.000 con số lẻ của số Pi

Ngày 19 tháng 9 năm 1995 lúc 0 giờ 29 phút giờ địa phương GMT-04, nhà Toán học Gia Nã Ðại Simon Plouffe đã khám phá cùng với sự hợp tác của Peter Borwein và David Bailey một công thức tính con số Pi đã làm đảo lộn một số ý kiến về số Pi được tính từ trước đến nay.

Công thức này được đặt tên là Công thức BBP cho phép tính các số lẻ của Pi độc lập với nhau, mà mọi người lúc bấy giờ tưởng là không thể tính các số lẻ một cách độc lập được.


 Fabrice Bellard tìm ra hôm thứ hai ngày 22 tháng 9 năm 1997 đã chiếm kỷ lục kiếm tới số lẻ thứ một ngàn tỉ cho con số Pi nhờ công thức BBP của Plouffe và nhờ tự nghiên cứu ra cách tính nhanh hơn.

Thứ ba tháng 2 năm 1999, Colin Percival đạt đến số lẻ thứ bốn mươi ngàn tỉ bằng cách dùng công thức của Bellard

11 tháng  9 năm  2000: con số lẻ thứ một triệu tỉ là số không (zero): (một triệu tỉ =1.000.000.000.000.000)

Bây giờ với máy tính chạy gấp mấy ngàn lần nhanh hơn, nhưng số Pi chỉ được tính xấp xỉ mà thôi bởi vì dãy số lẻ ấy vẫn chưa dừng lại.

 

           © http://vietsciences.free.fr  và http://vietsciences.org và http://vietsciences.net Võ Thị Diệu Hằng