Thật lạ là mỗi khi mời tôi đánh trống (thỉnh thoảng thôi), người nhạc trưởng lại thấy không cần thiết phải giới thiệu tôi còn làm cả vật lý lý thuyết nữa. Tôi giải thích điều đó là do chúng ta chuộng nghệ thuật hơn khoa học. Các họa sĩ thời Phục Hưng bảo rằng con người trước hết phải quan tâm tới chính con người, nhưng trong vũ trụ còn biết bao vật lý thú khác. Chả thế mà các họa sĩ lại ca ngợi cảnh Mặt Trời lặn, các lớp sóng nhấp nhô trên Đại Dương, các vì sao nhảy múa trên bầu trời... Vì vậy cũng không sao ngăn được họ nói chuyện ít nhiều về những hiện tượng ấy. Khi ngắm chúng, ta có những cảm xúc về cái đẹp. Nhưng ngoài ra, trong các hiện tượng tự nhiên còn có những hình thái và nhịp điệu không lọp vào con mắt của kẻ ngắm cảnh, nhưng lại bày ra rõ ràng trước mắt của nhà phân tích. Các hình thái và nhịp điệu ấy gọi là các định luật vật lý.
Trong bài giảng này, tôi muốn nói môt ít về những đặc diểm của một định luật vật lý nói chung, đứng cao hơn bản thân các định luật một mức mà nhìn xuống. Trước mắt tôi luôn luôn là một bức tranh của tự nhiên, bức tranh này chỉ hình thành sau một quá trình phân tích tỉ mỉ, nhưng tôi chỉ xin nói tới những nét chung nhất, chính nhất của bức tranh ấy mà thôi.
Dĩ nhiên một đề tài như vậy rất tổng quát và chỉ thích hợp với triết học. Nhưng tôi sẽ cố gắng trình bày cụ thể, bởi vì tôi cho rằng, một ý nghĩ đơn giản mà được diễn đạt trung thực sẽ có ích hơn nhiều lời nói xa xôi không rõ ràng. Vì vậy, trong bài giảng đầu tiên tôi sẽ không đi vào những lý luận tổng quát, mà chỉ nói tới một định luật vât lý để các bạn có được, dù chỉ là một thí dụ làm cơ sở cho các câu chuyện trừu tượng về sau. Tôi sẽ nhiều lần, nhiều lần trở lại thí dụ đó: hoặc để minh họa ý kiến mình, hoặc để làm bằng chứng cho những điều mà nếu không có thí dụ ấy nó sẽ hóa ra trừu tượng mất. Thí dụ đó, tôi đã chọn các vật hút lẫn nhau: định luật vạn vật hấp dẫn. Vì sao lại chọn nó, tôi cũng không biêt. Có thể vì định luật vĩ đại ấy là một trong những định luật được phát hiện đầu tiên và cómột lịch sử lý thú. Bạn sẽ bảo: "Vâng. Nhưng đó là câu chuyện đã cũ, mà chúng tôi lại muốn nghe một cái gì hiện đại hơn trong khoa học". Có thể sẽ mới hơn, nhưng không hiện đại hơn đâu. Khoa học hiện đại cũng nằm trong chính bản thân định luật hấp dẫn. Nói cách khac, thì chỉ muốn nghe về những phát minh mới. Còn tôi, tôi cứ muốn kể cho bạn về định luật vạn vật hấp dẫn, bởi vì khi trình bày lịch sử, con đường và phương pháp phát minh ra nó, những đặc điểm cơ bản của nó, tôi vẫn là một con người hoàn toàn hiện đại.
Định luật vạn vật hấp dẫn nói rằng hai vật tương tác lẫn nhau với một lực tỷ lệ nghịch với bình phương khoảng cách giữa chúng và tỷ lệ thuận với các khối lượng. Về mặt toán học, ta có thể biểu diễn định luật vĩ đại ấy bằng công thức:
F = G.mm'/r²
Một hằng số nào đó nhân với tích hai khối lượng và chia cho bình phương khoảng cách. Giờ nếu nhớ lại rằng dưới tác dụng của lực, vật sẽ được tăng tốc và độ biến thiên vận tốc sau một giây tỷ lệ nghịch với khối lượng -nghĩa là vận tốc biến đổi càng chậm khi khối lượng càng lớn- thì tôi có thể chỉ ra tất cả những gì cần nói về định luật hấp dẫn. Tất cả những cái còn lại chẳng qua chỉ là hệ quả toán học của hai điều đó mà thôi. Song, tôi biết rằng đối với những nhà không phải là toán học thì rất khó thấy hết các hệ quả đó; vì vậy tôi sẽ cố gắng kể vắn tắt về lịch sử và phát minh ra các định luật ấy, về một vài hệ quả của nó, về ảnh hưởng của nó tới lịch sử khoa học, về những điều bí mật mà nó đã làm cho sáng tỏ, về những điểm chính xác hóa mà Einstein đã nêu ra, và có thể, về mối liên hệ giữa định luật ấy với những định luật khác của vật lý.
Lịch sử của định luật tóm tắt vài nét như sau: quan sát chuyển động các hành tinh trên bầu trời, những người cổ xưa đã đoán rằng chúng cùng với Quả Đất quay quanh Mặt Trời. Sau dó, khi con người đã quên mất điều mà mình biết trước đây, thì đến lượt Copernic lại phát minh ra nó. Và bây giờ một câu hỏi mới đặt ra: các hành tinh quay quanh Mặt Trời cụ thể ra sao, chuyển động của chúng thế nào? chúng quay theo đường tròn và Mặt Trời nằm ở tâm hay lại chuyển động theo một đường cong nào khác? Chúng quay nhanh đên mức nào? v..v.. Làm sáng tỏ những điều ấy không phải là ngày một, ngày hai. Sau Copernic lại là những thời ky hỗn độn và nổ ra các cuộc tranh cãi dữ dội ở chỗ là các hành tinh cùng với quả đất quay quanh Mặt Trời, hay chính quả Đất là tâm của vũ trụ? Bấy giờ có người tên là Tycho Brahe đã nghĩ ra cách trả lời cho câu hỏi đó. Ông quyết định phải theo dõi rất kỹ xem hành tinh đã xuất hiện ở nơi nào trên bầu trời và ghi lại một cách chính xác, à chỉ bấy giờ mới có thể chọn cái nào trong hai lý thuyết đang xung khắc nhau. Đó chính là điều mở đầu cho khoa học hiện đại, là chìa khóa dãn tới các hiểu biết đúng đắn về tự nhiên: quan sát đối tượng cần nghiên cứu, ghi lại mọi chi tiết và hy vọng rằng những tài liệu thu được đó sẽ là cơ sở kiểm tra lý thuyết. Và như vậy là Tycho, một người giàu có, chủ nhân một hòn đảo gần Copenhagen, đã trang bị cho đảo của mình những vòng tròn lớn bằng đồng. Xây dựng các trạm quang trắc đặc biệt và đêm này qua đêm khác ghi lại vị trí của các hành tinh. Mọi phát minh đều chỉ có thể đạt tới bằng cả một chuỗi lao động cần cù mà thôi.
Khi các số liệu như vậy được tập hợp đầy đủ thì chúng lại rơi vào tay của Kepler, là người cố gắng giải vấn đề chuyển động của các hành tinh quanh Mặt Trời. Kepler tìm cách gỉi bằng phương pháp "thử và sai". Có một lần ông cho biết rằng ông đã tìm được lời giải: các hành tinh chuyển động theo đường tròn, nhưng Mặt Trời lại không nằm ở tâm. Sau đó, Kepler nhận thấy rằng một hành tinh - hình như là sao Hỏa- lệch đi 8 phút góc ra khỏi vị trí phải có của nóvà hiểu rằng lời giải trên không đúng, bởi vì Tycho Brahe không thể phạm một sai số lớn đến thế. Coi các kết quả quan sát là chính xác, ông quyết định phải xét lại lý thuyết của mình và cuối cùng tìm được ba sự kiện.
Trước hết, ông thấy rằng các hành tinh chuyển động quanh Mặt Trời theo những đường ellipse và Mặt Trời nằm tại một tiêu điểm của ellipse, đó là một đường cong mà mọi họa sĩ đều biết, bởi vì nó chính là một đường tròn kéo dẹt ra. Các trẻ em cũng biết: người ta đã bảo chúng rằng nếu luồn một sợi chỉ qua cái vòng, giữ chặc hai đầu và cho vào trong vòng một cái bút chì, thì nó vẽ nên đường ellipse.
Hai điểm A và B là hai tiêu điểm. Quỹ đạo hành tinh là hai ellipse. Mẵt Trời nằm tại một tiêu điểm. Lại nảy ra một câu hỏi khác: hành tinh chuyển động theo ellipse như thế nào? Lúc gần Mặt Trời nó có đi nhanh không? Khi xa Mặt Trời chuyển động của nó có chậm lại không? Kepler cũng đã trả lời được câu hỏi ấy (*).
Ông nhận thấy rằng, nếu lấy hai vị trí hành tinh ở cách nhau một khoảng thời gian nhất định , ba tuần lễ chẳng hạn, sau đó lấy một đoạn khác trên quỹ đạo và ở đây hai vị trí hành tinh cũng cách nhau ba tuần lễ và vẽ các đường (các nhà bác học gọi chúng là vectơ tia) nối Mặt Trời với hành tinh, thì diện tích gồm giữa quỹ đạo của hành tinh và mỗi cặp đường cách nhau ba tuần lễ như vậy ở bất kỳ phần nào của quỹ đạo cũng như nhau. Mà muốn các diện tích ấy như nhau thì hành tinh phải đi nhanh khi nó ở gần Mặt Trời, và đi chậm hơn khi ở xa nó.
Vài năm sau; Kepler nêu lên quy tắc thứ ba (*) không liên quan tới chuyển động của một hành tinh quanh Mặt Trời, mà liên quan tới các chuyển động của các hành tinh khác nhau. Quy tắc ấy cho biết rằng thời gian quay đúng một vòng của hành tinh quanh Mặt Trời phụ thuộc vào độ rộng của quỹ dạo, nó tỷ lệ với căn bậc hai của lập phương độ rộng ấy. Độ rộng của quỹ đạo là đường kính đi qua chỗ rộng nhất của ellipse . Như vậy Kepler đã phát minh ba định luật (*) mà ta có thể ghép lại làm một mà ta phát biểu là: quỹ đạo hành tinh là ellipse mà sau những khoảng thời gian bằng nhau thì đuờng nối Mặt Trời và hành tinh quét những diện tích bằng nhau và thời gian quay trọn vòng tỷ lệ với lũy thừa ba phần hai độ rộng của quỹ đạo., tức là căn bậc hai của lập phương độ rộng quỹ đạo. Ba định luật ấy của Kepler mô tả một cách đầy đủ chuyển động của hành tinh quanh Mặt Trời.
Bạn hãy tự hỏi: Cái gì đã buộc các hành tinh chuyển động quay quanh Mặt Trời? Thời Kepler, có người bảo là do phía sau mỗi hành tinh có những vị thần ngồi ở đó, vẫy đôi cánh tay và đẩy hành tinh chạy trên quỹ đạo. Sau này bạn sẽ thấy câu trả lời ấy không đến nỗi quá xa sự thật. Chỉ có một điều khác là các "vị thần" ngồi ở một chỗ khác và đẩy hành tinh về phía Mặt Trời.
Cũng trong thời gian ấy, Galilée nghiên cứu các định luật chuyển động của những vật thông thường mà ông có trong tay. Khi nghiên cứu các định luật ấy, ông đã tiến hành các thí nghiệm khác nhau để làm sáng tỏ quả cầu lăn như thế nào trên mặt phẳng nghiêng, con lắc lắc lư như thế nào v..v.. Galilée đã phát minh ra một nguyên lý vĩ đại gọi là nguyên lý quán tính mà nội dung là: nếu không có gì tác dụng lên một vật đang chuyển động với một vận tôc xác định theo đường thẳng thì nó sẽ chuyển động với chính đường thẳng đó và trên chính đường thẳng đó mãi mãi. Điều đó thật là lạ lùng đối với ai muốn thử ép buộc một quả cầu lăn mãi trên mẵt đát, nhưng nếu sự lý tưởng hóa ấy là đúng và không có gì tác dụng (chẳng hạn như ma sát của mặt sàn) lên vật, thì vật ấy sẽ mãi mãi lăn với một vận tốc không đổi.
Sai đó là đến lượt Newton, ông suy nghĩ về câu hỏi này: Nếu quả cầu không lăn theo đường thẳng thì bấy giờ thế nào? Và ông trả lời: muốn biến đổi vận tốc thì phải có lực. chẳng hạn nếu ta đẩy quả cầu theo hướng nó đang chuyển động thì nó sẽ lăn nhanh lên. Nếu bạn nhận thấy nó quay sang một bên thì có nghĩa là lực tác dụng vào bên sườn của nó. Lực có thể đo được bằng tích của hai đại lượng. Vận tốc biến đối đi bao nhiêu sau một đơn vị thời gian? Đại lượng ấy gọi là gia tốc. Nếu nhân nó với một hệ số gọi là khối lượng của vật thì tích co được sẽ là lực. Như vậy lực là đo được. Thí dụ như ta buộc hòn đá vào sợi dây và đem quay nó trên đầu thì ta có cảm giác là phải kéo sợi dây lại. Thật vậy khi hòn đá quay theo đường tròn, độ lớn của vận tốc không thay đổi, nhưng hướng thì thay đổi. Điều đó co nghia là cần có một lực luôn luôn kéo hòn đá vào tâm, mà lực đó thì tỷ lệ với khối lượng. Ta lấy hai vật khác nhau và đầu tiên cầm quay một vật, sau đó quay vật thứ hai với vận tốc như trước; trong trường hợp sau, khối lượng của vật thứ hai lớn hơn vật thứ nhất bao nhiêu lần thì lực cần thiết phải lớn hơn bấy nhiêu lần. Vậy nếu xác định được lực cần thiết để biến đổi vận tốc của vật, ta có thể tính khối lượng của nó. Vì thế Newton cho rằng, đối với hành tinh quay quanh Mặt Trời để chuyển động phía trước thì không cần có lực nào cả, nếu chẳng có lực nào tác dụng cả thì hành tinh sẽ đi theo đường tiếp tuyến với quỹ đạo chuyển động. Nhưng đằng này nó lại không đi theo đường thẳng. Nó như luôn luôn không ở vào chỗ phải có của nó khi chuyển động tự do, mà bị kéo vào gần Mặt Trời
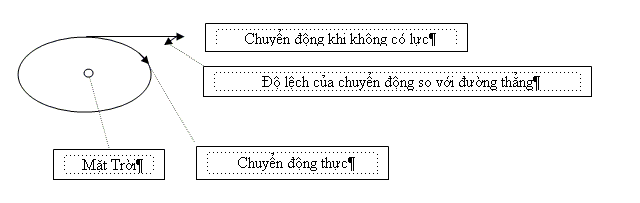
Nói cách khác, vận tốc và chuyển động của ó lệch về phía Mặt Trời. Vì vậy "vị thần" phải vẫy cánh thế nào để luôn luôn đẩy hành tinh về phía Mặt Trời.
Nhưng chuyển động tự do thì không có một nguyên nhân rõ ràng nào cả. Vì sao các vật lại có khả năng chuyển động mãi mãi theo đường thẳng, điều đó chúng ta không biết. Nguồn gốc của định luật quán tính đến nay còn là một điều bí ẩn. Không có các vị thần nhưng chuyển động tự do thì vẫn tồn tại và muốn bẻ cong nó thì cần thiết phải có lực. Rõ ràng là nguồn lực ở đâu đấy gần Mặt Trời. Vá Newton đã chứng minh rằng định luật thứ hai của Kepler -định luật về sự bằng nhau của các diện tích- chỉ là một hệ quả trực tiếp của ý kiến đơn giảnlà mọi biến đổi của vận tốc đều hướng về Mặt Trời. Cả trong trường hợp quỹ đạo ellipse cũng thế. Trong bài giảng sau, tôi sẽ cố gắng giải thích chi tiết làm sao rút ra được các hệ quả đó.
Định luật ấy củng cố ý nghĩ của Newton cho rằng lực hướng về phía Mặt Trời và nếu biết chu kỳ quay của các hành tinh khác nhau phụ thuộc vào khoảng cách tới Mặt Trời như thế nào thì có thể xác định lực giảm ra sao theo khoảng cách. Ông đã tìm thấy lực tỷ lệ nghịch với bình phương khoảng cách.
Tới đó Newton cũng chưa nói lên điều gì mới mà bằng những lời lẽ khác lập lại điều mà Kepler đã nói trước mà thôi. Một định luật Kepler tương đương với khẳng định rằng lực hướng về phía Mặt Trời, còn một định luật khác thì tương đương với khẳng định ràng lực tỷ lệ nghịch với bình phương khoảng cách.
Còn người nhìn qua ống viễn vọng ngắm sao Mộc cùng với các vệ tinh bị hút về phía sao mộc. Mặt Trăng cũng quay quanh Quả Đất và bị hút về phía Quả Đất hoàn toàn giống như thế. Dĩ nhiên một ỳ nghĩ nảy ra là tính hấp dẫn tồn tại ở khắp nơi. Vấn đề còn lại chỉ là tổng quát hóa các điều quan sát và phát biểu là: mọi vật đều hút lẫn nhau. Như vậy Quả Đất phải hút Mặt Trăng giống như Mặt Trời hút các hành tinh. Song ai cũng biết rằng Quả Đất hút cả những vật thông thường: chẳng hạn như bạn ngồi vững vàng trên ghế mặc dù có thể bạn lai muốn bay lên không trung kia. Tính hấp dẫn của các vật về phía Quả Đất là một hiện tượng ai cũng biết rõ. Newton giả thiết rằng, có những lực giống như lực hút các vật về phía Quả Đất đã giữ cho Mặt Trăng quay trên quỹ đạo của nó.
Mỗi giây Mặt Trăng rơi xuống bao nhiêu, điều đó cũng chẳng khó hình dung, bởi vì bạn biết kích thước quỹ đạo, biết Mặt Trăng quay trọn vòng quanh Quả Đất trong một tháng, tính xem nó đi được bao nhiêu trong một giây, bạn có thể thấy rõ sau một giây, đường tròn quỹ đạo Mặt Trăng sẽ lệch đi bao nhiêu so với đường thẳng mà theo đó Mặt Trăng sẽ chuyển động nếu như Quả Đất không hút nó. Đại lượng này hơi lớn hơn 1,25 mm một chút. Mặt Trăng ở 60 lần xa tâm Quả Đất hơn chúng ta (chúng ta ở cách tâm quả đất 6400km, cón Mặt Trăng thì cách 378000km). Nếu định luật về sự tỷ lệ nghịch với bình phương khoảng cách mà đúng thì vật ở gần mặt đất phải rơi được 1,25.60² sau một giây, bởi vì ở vị trí quỹ đạo Mặt Trăng các vật phải bị hút 60x60 lần yếu hơn. Vậy là 1,25mmx3600, tức vào khoảng 5m. Các phép đo của Galilée cho thấy vật rơi ở gần mặt đất đi được 5m sau một giây. Điều đó có nghĩa là Newton đúng, bởi vì nếu trước đây ta biết được hai sự kiện độc lập với nhau -thứ nhất là chu kỳ quay của Mặt Trăng và độ rộng quỹ đạo của nó, và thứ hai là khoảng cách mà vật rơi ở gần mặt đất đi được trong một giây- thì bây giớ các sự kiện ấy bị ràng buộc với nhau rất chặc chẽ. Sự kiểm nghiệm lý thú ấy chứng tỏ tất cả đều phú hợp với lý thuyết của Newton.
Sau đó, Newton đưa ra thêm một số dự đoán khác. Ông đã tính được hình dạng của quỹ đạo phải thế nào nếu như định luật về sự tỷ lệ nghịch với bình phương khoảng cách là đúng. Ông đã tìm thấy rằng quỹ đạo phải là ellipse và đó là sự kiện thứ ba chứng minh cho định luật của ông. Ngoài ra, Newton còn giải thích được một số hiện tượng khác nữa.
Trước tiên là hiện tượng thủy triều. Thủy triều do mặt trăng hút Quả đất cùng các đại dương của nó gây nên. Từ trước, người ta vẫn nghĩ thế, song có một điều chưa giải thích được: nếu Mặt trăng gút nước và làm nó dâng lên ở phía Quả đất gần Mặt trăng thì trong một ngày đêm chỉ có thể xảy ra một lần thủy triều mà thôi -ở phần mặt của quả đất quay về phía Mặt trăng
(còn tiếp)
Bài đọc thêm:
(*) Ðịnh luật thứ I và II Kepler
(*) Ðịnh luật thứ III Kepler và cách tính khối lượng các thiên thể
Hệ thống Copernic và ảnh hưởng
Lực Hấp Dẫn , tác giả Trịnh Xuân Thuận
© http://vietsciences.free.fr Hoàng Quý và Phạm Quý Tư dịch